|
|
UN POCO DE TEORÍA
Para empezar, servidor no es ningún genio matemático, por lo que voy a intentar explicar las conclusiones a las que he llegado después de releer mil paginas y artículos.
Las reglas de calculo se basan en los logaritmos, una definición matemática de logaritmo seria : "el logaritmo de x con base b, es el exponente o potencia a la que la base se ha de elevar para dar un número dado".
En una ecuación bn=X, el logaritmo es la función que obtiene n. Un ejemplo: 24=16 log216=4 el logaritmo son las veces que tenemos que dividir x (16) por su base (2) para obtener 1, en este caso 4.
ln(x), log(x) y loge(x) (log o LOG en informática) se usan para describir el logaritmo natural de x.
log10(x) se usa para describir el logaritmo en base 10.
A lo "matemática bestia": Un logaritmo es un numero que define a otro...(prometo que lo he visto escrito en alguna parte...), para conocer el logaritmo de un numero no hay que volverse loco calculando, antiguamente se publicaban libros (las conocidas "tablas de logaritmos") para facilitar la tarea y actualmente con una calculadora o un ordenador hay de sobras, un ejemplo seria la:
Minicalculadora logarítmica
La "gracia" de los logaritmos reside en que la suma de los logaritmos de dos números da como resultado otro numero (también logarítmico), que pasado a numero real seria su multiplicación...: (pon dos números en las casillas rojas y pulsa en el signo + para calcular).
A esto se le llama la propiedad fundamental ln(ab) = ln(a) + ln(b), y es la base de las reglas de calculo.
¿Y la división?, fácil, es lo contrario: en vez de sumar, restaríamos :ln(a/b) = ln(a) - ln(b)
Antiguas películas americanas en 16 mm en donde se explican los fundamentos básicos de las Reglas de Calculo (YouTube, en Ingles)
  
  
Mas información en este enlace al foro ARC
Ver también los links en la sección de reglas virtuales, muy interesantes para probar y practicar
Dibujamos una regla logarítmica: (el 2 esta a 3,01cm del 1, el 3 a 4,77cm del 1, el 4 a 6,02cm del 1, etc.., utilizar la minicalculadora)
La cortamos y lo colocamos así, por ejemplo:
¿Que resulta?, pues que al encarar el 1 de la regla de abajo con el 2 de la regla superior tenemos el multiplicando (el 2), las cifras de la regla inferior se convierten en el multiplicador y el resultado aparece encima de ellas..., ¿y la división?, pues si tomamos las cifras de la regla superior como del dividendo y la inferior como divisor podemos ver el resultado encima del 1 de la regla inferior...
Así aparecen en el reverso de una Faber Castell Mentor 52/80 las reglas básicas:
DESCRIPCIÓN DE LOS MÉTODOS BÁSICOS A EMPLEAR EN UNA REGLA DE CALCULO
Aprovechando el manual de instrucciones del modelo 692 de Graphoplex, voy a ir poniendo fotos reales siguiendo la descripción (Por ahora son pruebas para encontrar la mejor forma de visualizarlo).
AQUÍ se puede jugar con una Pickett N600-ES virtual y probar todo esto, al poco que se practique puede entenderse perfectamente...
RESOLUCIÓN DE ECUACIONES DE 2º GRADO
En esta pagina se puede ver un fenomenal trabajo de Fernando Tejon sobre la resolución de ecuaciones de 2º grado, que complementa al libro de Diego Velásquez. Publicado con permiso expreso del autor.
UNAS TABLAS "RÁPIDAS":
Unas fantásticas tablas, extraídas del libro de
Diego Velásquez,
no hay excusa para coger la regla, quitarle el polvo y probar....
OTRAS TABLAS "RÁPIDAS":
MAS COSAS... Tablas con una variable
Con las anteriores tablas se puede adivinar "lo potente" que puede ser una Regla de Calculo por la interacción entre las escalas y el movimiento de cursor y reglilla.
Pero para hacerse todavía con una idea mejor:
En una Regla de Calculo las escalas están alineadas longitudinalmente, pero si las enfrentáramos entre si obtendríamos la siguiente tabla:
Tabla extraída de un fantástico articulo publicado por Peter Alfeld
Se pueden ver todas las formulas posibles que directamente generan las escalas "básicas"...
Ejemplo: tomemos x=4, buscamos con el cursor el 4 en la escala A ó B y sin moverlo, veremos los resultados con las formulas aplicadas en las otras escalas: En la casilla
1 En la casilla
2 En la casilla
3 En la casilla
4
Al igual que en la anterior tabla ¿A
que espera a probar...? ¿Verdad que es complicado con una calculadora... Agradecería comentarios y mejoras
sobre estas explicaciones..., o lo que es lo mismo: ¿Se entiende algo...?
Si de esta manera se ve fácil y comprensible podría ir añadiendo mas operaciones "visuales". (Gracias a Eugenia, que me hado la idea... :-))
Y PARA TERMINAR... (aun hay mas, pero para otro día...)
UN POCO DE HISTORIA
(de la Wikipedia, ver también las presentaciones de colaboradores ARC)
Joost Bürgi, un matemático y relojero suizo al servicio del Duque de Hesse-Kassel, concibió por vez primera los logaritmos. El método de logaritmos naturales fue propuesto inicialmente en 1614, en un libro intitulado Mirifici Logarithmorum Canonis Descriptio, por John Napier (latinizado Neperus), Barón de Merchiston en Escocia, que nació cerca de 1550, y murió en 1618, cuatro años después de la publicación de su memorable invención. Este método contribuyó al avance de la ciencia, y especialmente de la astronomía, facilitando la realización de cálculos difíciles. Antes del advenimiento de las calculadoras y computadoras, era constantemente usado en estadística, navegación, y otras ramas de las matemáticas prácticas. Además de su utilidad en el cómputo, los logaritmos también llenaron un importante lugar en las matemáticas avanzadas mayores.
La palabra logaritmo, que se debe a Napier, está formada de las palabras griegas λογος (logos), que significa razón o cociente, y αριθμoς (arithmos), con el significado de número, y se define, literalmente, como un número que indica una relación o proporción. Se refiere a la proposición que fue hecha por Napier en su teorema fundamental, que establece que la diferencia de dos logaritmos determina la relación de los números a los cuales corresponden, de manera que una serie aritmética de logaritmos corresponde a una serie geométrica de números.
Desde 31-03-2011
|














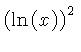

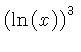





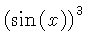


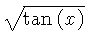

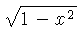
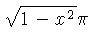
![$ \sqrt [4]{1-{x}^{2}} $](teoriapractica/sgif/simg140.gif)

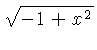
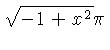
![$ \sqrt [4]{-1+{x}^{2}} $](teoriapractica/sgif/simg152.gif)



